Valuing Wal-Mart 2010 – Case Solution

Case questions answered:

Not the questions you were looking for? Submit your own questions & get answers.

Valuing Wal-Mart 2010 Case Answers

This case solution includes an Excel file with calculations.

Executive Summary – Valuing Wal-Mart 2010

We have evaluated Wal-Mart’s stock value using five methods, which are DDM, two-stage DDM, three-stage DDM, P/E ratio, and FCFE. However, we choose three-stage DDM as the best method to value stock. Such a method can evaluate the stock at $89.34 while the current price is $53.45.

This means Wal-Mart’s stock price is supposed to be $89.34 instead. Therefore, the stock is actually undervalued. This leads us to the ‘BUY’ suggestion with a target price of $89.34, along with an upside of 67%.

The reason we chose three-stage DDM is. First, the firm continuously pays a dividend. Second, the data given is enough to cover the estimation, which allows a more precise valuation. Third, separating dividends into three stages can lead to more punctual prediction than one or two-stage DDM. However, Wal-Mart has been increasing its dividend.

According to Informational Signaling Theory, paying more dividends also signals the manager’s confidence in cash flows. Furthermore, according to the Agency Cost Model, increasing dividends also signals that the manager tends not to hoard excess cash (which helps to avoid agency problems). These are also the reasons why clients should take the BUY position.

Introduction

Sabrina Gupta, an investment advisor, is deciding whether to advise her clients to buy Wal-Mart’s stock. To solve this challenge, we use several valuation methods, including DDM, two-stage DDM, and three-stage DDM, FCFE, and P/E ratio.

1. The Perpetual Growth: Dividend Discount Model

DDM method is used based on the assumptions as follows. First, Wal-Mart is growing with a stable growth rate. To explain, we assume that the growth rate in dividends is perpetual. Furthermore, the firm’s other performance (i.e., earnings) should grow at the same rate. Second, the growth rate must not exceed the cost of equity.

Value of Stock = D1/(k_e-g) = $1.21/(6.99% – 5%) = $60.82

In the case of the expected dividend, we use $1.21 (a consensual estimation from analysts). In addition, we also obtain the expected constant dividend growth rate from one respected analyst. Such a rate is 5%.

However, for the cost of equity, we use CAPM to acquire the value. In terms of the risk-free rate, we use 3.68% (long-term 10-year government bond yield.)

For market risk premium, we use 5.05% (given by Bloomberg). Also, we use an adjusted beta made by Bloomberg, representing a forward-looking view that is 0.655. Now, we can calculate the cost of equity at 6.99%.

All in all, Wal-Mart’s stock value using the DDM method is $60.82.

2. The Two-Stage Dividend Discount Model

The model is comprised of two stages. In the first stage, it is assumed that the firm’s dividend will grow rapidly. The second stage has a length that equals the remaining years after the first stage. In this stage, dividend growth is assumed to be lower and stable.

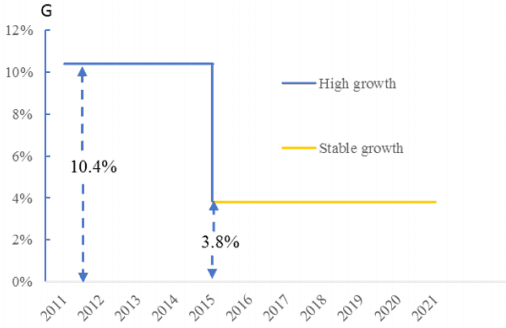
a. DDM Calculation during the first stage (the year 2011 – 2015)

In this case, the first stage is assumed to cover 5 years. In 2011, the expected dividend estimated by analysts was $1.21. In terms of growth rate, we use the earning growth rate predicted by the analysts, that is, 10.40% [See Appendix I].

For the years 2011 – 2015, we get the expected dividend as $1.21, $1.33, $1.47, $1.62, and $1.79, respectively. Therefore, we can now discount each amount to find out the present value. (Discount as 6.99% derived from CAPM. [See Page 1: DDM method].) Lastly, the total present value for the first stage is $6.03.

b. DDM Calculation during the second stage (the year 2016 onwards)

Stable Growth Rate = (1 – Payout Ratio)*Cost of Equity

= (1 – 45%)*6.91% = 3.80%

We use the payout ratio at maturity given by the case, which is 45%. In the case of the cost of equity, we use CAPM to generate. The inputs we apply in CAPM are the same ones we used in the CAPM equation in the DDM method, except for beta.

In terms of beta, we do not use the adjusted beta given by the case since we think that during maturity, the firm’s risk should be changed due to the new capital structure. Therefore, we un-lever the 2010 raw beta (beta = 0.483).

Then, re-lever it using Wal-Mart’s 2015 projected debt to the equity, which is 41%. Consequently, we get a 2015 Raw Beta, which is 0.46. To obtain the Adjusted 2015 Beta, we calculate this equation [See Appendix II]. The new Adjusted 2015 Beta is 0.64. We then can apply it to the CAPM equation.

(Rf = 3.68%, MRP = 5.05% and 2015 Adjusted Beta = 0.64)

Finally, we came up with the cost of equity for the maturity stage as 6.91%.

Terminal value for the second stage

= D0(1+g)/(Ke – g)

= $1.80*(1+3.80%)/(6.91% – 3.80%) = $60.03

Once we acquire terminal value, we discount it to get the…